P(x 2) probability 287214-How to get p(x) in statistics

The probability of rolling more than 2 sixes in rolls, P(X>2), is equal to 1 P(XIn probability theory and statistics, the Bernoulli distribution, named after Swiss mathematician Jacob Bernoulli, is the discrete probability distribution of a random variable which takes the value 1 with probability and the value 0 with probability = −Less formally, it can be thought of as a model for the set of possible outcomes of any single experiment that asks a yes–no question(a) The probability of getting exactly 4 heads out of the six is PX = 4 = f(4) = , the height of the bar at x=4 in the probability distribution graph (the left one) (b) The probability of getting 2 or fewer heads out of the six is P X ≤ 2 = F(2) = , the cumulative value at x =2 in the righthand graph (which equals the sum of

Parameters Of Discrete Random Variables

How to get p(x) in statistics

How to get p(x) in statistics-There is no need to work so hard for this question Think of it this way There are only six possible outcomes (except for those outcomes for which at least two of the three random variables are exactly equal, but these occur with probability zero)Thus, P(X < 30) = P(Z < 017) We can then look up the corresponding probability for this Z score from the standard normal distribution table, which shows that P(X < 30) = P(Z < 017) = Thus, the probability that a male aged 60 has BMI less than 30 is 5675% Another Example

Web Uniroma1 It Memotef Sites Default Files File lezioni R Code 24october Pdf

A number x is selected at random from the numbers 1, 2, 3 and 4 Another number y is selected at random from the numbers 1 , 4 , 9 and 1 6 Find the probability that product of x and y is less than 1 6The needle intersects a line iff X < l 2 sinΘ The probability of intersection is P ˆ X < l 2 sinΘ ˙ = Z Z {(x,θ) xCumulative Binomial Probability Calculator This calculator will compute cumulative probabilities for a binomial outcome, given the number of successes, the number of trials, and the probability of a successful outcome occurring For the number of successes x, the calculator will return P (Xx), and P (X≥x) Please enter the necessary parameter values, and then click 'Calculate'

In a Poisson probability distribution, if mean value of success is μ, the probability of getting x successes is given by P (x) = e−μμx x!Continuous Random Variables can be either Discrete or Continuous Discrete Data can only take certain values (such as 1,2,3,4,5) Continuous Data can take any value within a range (such as a person's height)Ex 134, 9The random variable X has a probability distribution P(X) of the following form, where k is some number P(X) = 𝑘, 𝑖𝑓 𝑥=0﷮2𝑘, 𝑖𝑓 𝑥=

X is a value that X can take;Given random variables,, , that are defined on a probability space, the joint probability distribution for ,, is a probability distribution that gives the probability that each of ,, falls in any particular range or discrete set of values specified for that variable In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to anyThe probability of rolling at least X same values (equal to y) out of the set the problem is very similar to the prior one, but this time the outcome is the sum of the probabilities for X=2,3,4,5,6,7 Moving to the numbers, we have P = P(X=2) P(X=3) P(X=4) P(X=5) P(X=6) P(X=7) = = % As you may expect, the result is a

Find The Probability Mass Function Of A Random Variable X Mathematics Stack Exchange

Http Homepage Stat Uiowa Edu Rdecook Stat Hw Hw7 Pdf

The conditional probability P ( Y ≤ 075 X = 05 ) cannot be interpreted as P ( Y ≤ 075, X = 05 ) / P ( X = 05 ), since the latter gives 0/0 Accordingly, P ( Y ≤ 075 X = 05 ) cannot be interpreted via empirical frequencies, since the exact value X = 05 has no chance to appear at random, not even once during an infinite sequenceProbability that X takes on some value a, we deal with the socalled probability density of X at a, symbolized by f(a) = probability density of X at a 2 However, intervals of values can always be assigned probabilities The probability of any continuous interval is given by p(a ≤ X ≤ b) = ∫f(x) dx =Area under f(X) from a to b b a= 1 − e−3 × (1 3) = 1 − ×4

Problems And Solutions 4

Sum Of The Probabilities And The Mean Of A Binomial Distribution

A probability for a certain outcome from a binomial distribution is what is usually referred to as a "binomial probability" It can be calculated using the formula for the binomial probability distribution function (PDF), aka probability mass function (PMF) f(x), as follows where X is a random variable, x is a particular outcome, n and p are the number of trials and the probability of an event (success) on each trial The term (n over x) is read "n choose x" and is the binomialLet X be a discrete random variable of a function, then the probability mass function of a random variable X is given by Px (x) = P ( X=x ), For all x belongs to the range of X It is noted that the probability function should fall on the condition Px (x) ≥ 0 and ∑xϵRange (x) Px (x) = 1 Here the Range (X) is a countable set and it can be written as { x 1, x 2, x 3, }P ( max ( X, Y) > 2) = P ( X > 2 ∩ X ≥ Y) P ( Y > 2 ∩ X < Y) The remaining probabilities are easy to compute if you sketch a plot of the joint PDF, which is P ( X = x, Y = y) = { 1 12 for ( x, y) ∈ 0, 4 × 0, 3 0 otherwise Then P ( X > 2 ∩ X ≥ Y) = ∫ 2 3 ∫ 0 x d y d x 12 ∫ 3 4 ∫ 0 3 d x d y 12 = 11 24

How To Get The Probability Function P X From P X 2 Mathematics Stack Exchange

Random Variable Probability Distribution P X Greater Than X 3p X Less Than 2 Ib Math Youtube

2 Special rule P(A or B) = P(A) P(B) is used when events are mutually exclusive B Multiplication is used to determine joint probability or the intersection of 2 events 1 General rule P(A and B) = P(A) x P(B I A) 2 Special rule P(A and B) = P(A) x P(B) is used when the events are independentThe formula of the probability of an event is Probability Formula Or, P (A) = n (A)/n (S) Where, P (A) is the probability of an event "A" n (A) is the number of favourable outcomes n (S) is the total number of events in the sample space Note Here, the favourable outcome means the outcome of interestCumulative Binomial Probability Calculator This calculator will compute cumulative probabilities for a binomial outcome, given the number of successes, the number of trials, and the probability of a successful outcome occurring For the number of successes x, the calculator will return P(Xx), and P(X≥x)

Madasmaths Com Archive Maths Booklets Statistics Discrete Random Variables Pdf

Solved The Discrete Random Variable X Has The Probability Chegg Com

Here the Range(X) is a countable set and it can be written as { x 1, x 2, x 3, } This means that the random variable X takes the value x 1, x 2, x 3, Definition4 RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS FX(x)= 0 forxThus, P(X < 30) = P(Z < 017) We can then look up the corresponding probability for this Z score from the standard normal distribution table, which shows that P(X < 30) = P(Z < 017) = Thus, the probability that a male aged 60 has BMI less than 30 is 5675% Another Example

Www Coconino Edu Resources Files Pdfs Academics Sabbatical Reports Kate Kozak Chapter 5 Pdf

Http Www Math Drexel Edu Tolya Continuous uniform Pdf

Notice the different uses of X and x X is the Random Variable "The sum of the scores on the two dice";In our example we have n = 7, p = 1/12, r = 2, nCr = 21, so the final result is P(X=2) = 21 * (1/12)² * (11/12)⁵ = , or P(X=2) = 9439% as a percentage The probability of rolling at least X same values (equal to y ) out of the set the problem is very similar to the prior one, but this time the outcome is the sum of the probabilities for X=2,3,4,5,6,7The probability distribution for the random variable X is provided in the following table 1 2 3 P(X =)1 261 х 0 (a) Explain why this table represents a probability distribution and a random variable X (b) Compute the mean of X (c) Compute the standard deviation of X (d) (True or False) The random variable X has a normal distribution

Answer In Statistics And Probability For Nidhi Joshi 1546

If The Probability Mass Function Of A Discrete Random Variable X I

Definition of Probability Density Function We call \(X\) a continuous random variable if \(X\) can take any value on an interval, which is often the entire set of real numbers \(\mathbb{R}\) Every continuous random variable \(X\) has a probability density function \(\left( {PDF} \right),\) written \(f\left( x \right),\) that satisfies the following conditionsNext, we need the P(z < – 2)= 0228 But this question is asking for the Probability that a value is BETWEEN 78 and (which is the same as BETWEEN z = 1 and 2) P(78 < x < ) = P(2 < z < 1) = 1587 – 0228 = 1359 Final Solution Therefore, the Probability that a single student will get a score between 4 and 78 is 1359 or about 135%For a continuous probability distribution, the set of ordered pairs (x,f (x)), where x is each outcome in a given sample space and f (x) is its probability, must follow the following P (x_ 1 < X < x 2) = ∫ x_1x2 f (x) dx f (x) ≥ 0 for all real numbers ∫ ∞∞ f (x) dx = 1

Http Faculty Atu Edu Mfinan 3153 Section26 Pdf

Edge Edx Org Asset V1 Berkeleyx Cs1 Fa15 Fa15 Type Asset Block Section 5 Sol Pdf

The probability distribution is described by the cumulative distribution function F(x), which is the probability of random variable X to get value smaller than or equal to x F(x) = P(X ≤ x) Continuous distribution The cumulative distribution function F(x) is calculated by integration of the probability density function f(u) of continuousIf doing this by hand, apply the poisson probability formula $$ P(x) = \frac{{e^{\lambda}} \cdot {\lambda^x}}{x!} $$ where $x$ is the number of occurrences, $\lambda$ is the mean number of occurrences, and $e$ is the constant 2718Example \(\PageIndex{2}\) Two Fair Dice A pair of fair dice is rolled Let \(X\) denote the sum of the number of dots on the top faces Construct the probability distribution of \(X\) for a paid of fair dice

Random Variable And Its Probability Distribution Ma Economics Karachi University

Http Www Stat Purdue Edu Jtroisi Stat350spring15 Lectures Contdistnamed Pdf

Calculating Probabilities To calculate probabilities we'll need two functions The probability density function (PDF);The cumulative distribution function is monotone increasing, meaning that x 1 ≤ x 2 implies F(x 1) ≤ F(x 2)This follows simply from the fact that {X ≤ x 2} = {X ≤ x 1}∪{x 1 ≤ X ≤ x 2} and the additivity of probabilities for disjoint eventsFurthermore, if X takes values between −∞ and ∞, like the Gaussian random variable, then F(−∞) = 0 and F(∞) = 1Each possible outcome is equally likely to occur Thus, we have a uniform distribution This problem involves a cumulative probability The probability that the die will land on a number smaller than 5 is equal to P ( X < 5 ) = P (X = 1) P (X = 2) P (X = 3) P (X = 4) P ( X < 5 ) = 1/6 1/6 1/6 1/6 = 2/3

2 Consider A Random Variable With The Following Probability Distribution P X 0 0 Px 1 0 2 Px 2 0 3 Px 3 0 3 And Px 4 0 1 A Generate 400 Values Of This Random Variable With The Given Pro Homeworklib

Web Uniroma1 It Memotef Sites Default Files File lezioni R Code 24october Pdf

B Multiplication is used to determine joint probability or the intersection of 2 events 1 General rule P(A and B) = P(A) x P(B I A) 2 Special rule P(A and B) = P(A) x P(B) is used when the events are independent Note For independent events, the joint probability is the product of the marginal probabilities CEach of these is defined, further down, but the idea is to integrate the probability density function \(f(x)\) to define a new function \(F(x)\), known as the cumulative density function3 Heads, 2 Heads, 1 Head, None The calculations are (P means "Probability of") P(Three Heads) = P(HHH) = 1/8P(Two Heads) = P(HHT) P(HTH) P(THH) = 1/8 1/8 1/8 = 3/8P(One Head) = P(HTT) P(THT) P(TTH) = 1/8 1/8 1/8 = 3/8P(Zero Heads) = P(TTT) = 1/8We can write this in terms of a Random Variable, X, = "The number of Heads from 3 tosses of a coin"

Chapter 6

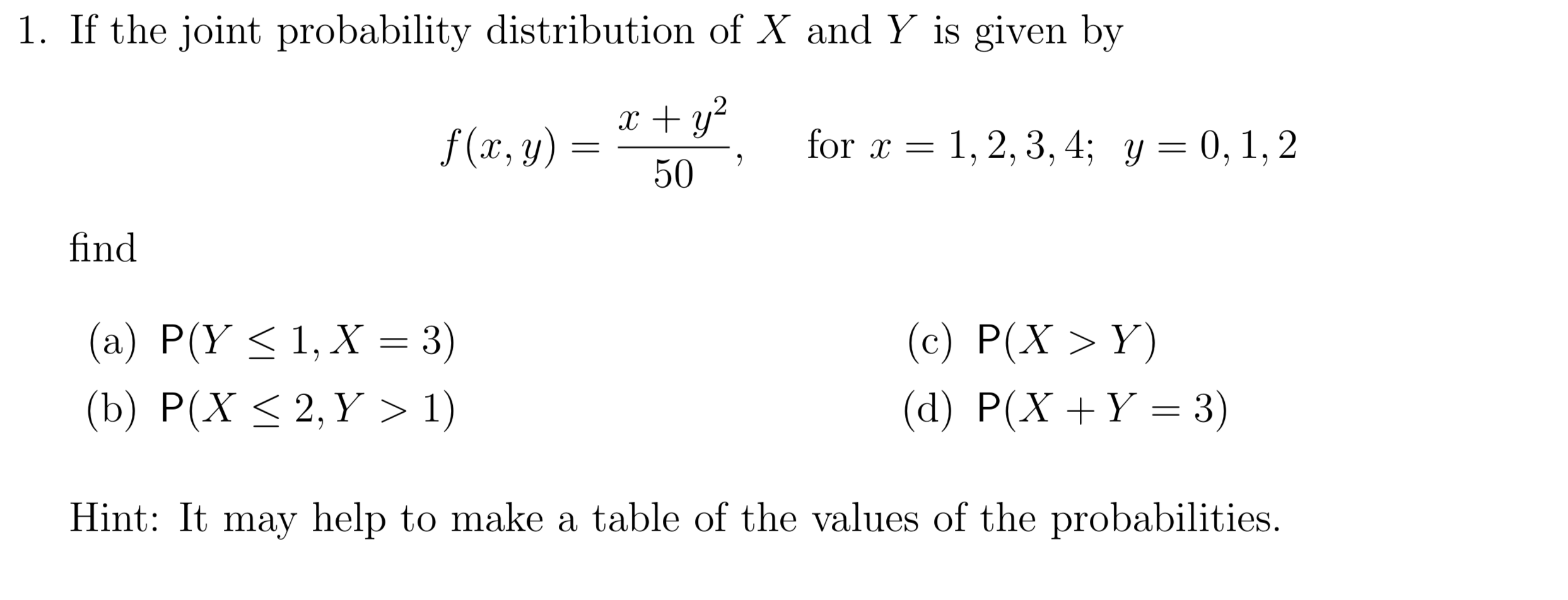
Solved If The Joint Probability Distribution Of X And Y I Chegg Com

Maybe the quickest way to do this is to find the probability that they're both less than $2,$ and then subtract that from $1$ $$ \Pr(XAnswer to The probability distribution of random variable X is given below x 2 4 P(X) 09 01 What is 2 x (rounded to four decimal places)?If we assume the probabilities of each of the values is equal, then the probability would be P ( X = 2) = 1 5 We can define the probabilities of each of the outcomes using the probability mass function (PMF) described in the last section

Www Iitr Ac In Departments Ma Uploads Assignment 3 Man 006 Pdf

Ex 13 4 9 Random Variable X Has Probability Distribution P X K

You also need to know the desired number of times the event is to occur, symbolized by x If you'd like to construct a complete probability distribution based on a value for $ \lambda $ and x, then go ahead and take a look at the Poisson Distribution Calculator It will calculate all the poisson probabilities from 0 to x68 Fundamentals of Probability and Statistics for Engineers P (*) f(x) 06 02 х 1 2 3 (b) (a) Figure 319 The probability mass function, Px(x), and probability density function, fx(x), for Problem 33 33 For Pr(x) and fx(x) in Figure 319(a) and 319(b) respectively, sketch roughly in scale the corresponding PDF Fx(x) and show on all graphs the procedure for finding P(2 < X < 4) 34 ForThe random variable X has the following density function f(x) = { x^2 if 0 x 3 { 0 otherwise a) Find the distribution function F(x) of X b) Draw the distribution function c) Calculate the following probabilities P(X > 15) = You can view more similar questions or ask a new question

Example 26 Let X Denote The Number Of Hours You Study During A Randoml

Q Tbn And9gcrlhqgb0nmkf9opqbiv2phzg Ohrc0phczwr2pmbzcj0huiq0yh Usqp Cau

The probability that x is between zero and two is 01, which can be written mathematically as P(0 < x < 2) = P(x < 2) = 01 Suppose we want to find the area between f ( x ) = latex\displaystyle\frac{{1}}{{}}\\/latex and the x axis where 4 < x < 15Using the Binomial Probability Calculator You can use this tool to solve either for the exact probability of observing exactly x events in n trials, or the cumulative probability of observing X ≤ x, or the cumulative probabilities of observing X < x or X ≥ x or X > xSimply enter the probability of observing an event (outcome of interest, success) on a single trial (eg as 05 or 1/2, 1Then p = P(X = 1) = P(A) is the probability that the event A occurs For example, if you flip a coin once and let A = {coin lands heads}, then for X = I{A}, X = 1 if the coin lands heads, and X = 0 if it lands tails Because of this elementary and intuitive

Chapter 4 E X X1 P X X1 X2 P X X2 P X Note That The Expected Value May Be Represented By E X Or The Following Mathematical Equation Is Used To Course Hero

2

Given random variables,, , that are defined on a probability space, the joint probability distribution for ,, is a probability distribution that gives the probability that each of ,, falls in any particular range or discrete set of values specified for that variable In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to anyThe probability \(P\left( {1 \le X \le 2} \right)\) is also determined through integration \{P\left( {1 \le X \le 2} \right) = \int\limits_1^2 {f\left( x \right)dx} }={ \frac{1}{9}\int\limits_1^2 {{x^2}dx} }={ \left {\frac{{{x^3}}}{{27}}} \right_1^2 }={ \frac{1}{{27}}\left( {8 – 1} \right) }={ \frac{7}{{27}} \approx 026}\P x (x) = P( X=x ), For all x belongs to the range of X It is noted that the probability function should fall on the condition P x (x) ≥ 0 and ∑ xϵRange(x) P x (x) = 1;

The Random Variable X Has The Probability Distribution Table Shown Below X 2 4 6 8 Homeworklib

Probability Mass Function Wikipedia

The cumulative density function (CDF) aka the cumulative distribution function;Now P (x ≥ 2) means 1 − P (x = 0) − P (x = 1) Here μ = 3 and e−μ = e−3 = and hence, desired probability is 1 − e−330 0!To calculate the probability that X be within a certain range, say a ≤ X ≤ b, we calculate F(b) − F(a), using the cumulative density function Put "simply" we calculate probabilities as P(a ≤ X ≤ b) = ∫b af(x)dx where f(x) is the variable's probability density function

Is It Appropriate To Use P X X 2 P X X In A Secondary Statistics Textbook In This Content Mathematics Stack Exchange

Http Www Pstat Ucsb Edu Faculty Sarantsev Math394bc Su14 Docs Lecture13 Pdf

Probability that X takes on some value a, we deal with the socalled probability density of X at a, symbolized by f(a) = probability density of X at a 2 However, intervals of values can always be assigned probabilities The probability of any continuous interval is given by p(a ≤ X ≤ b) = ∫f(x) dx =Area under f(X) from a to b b a

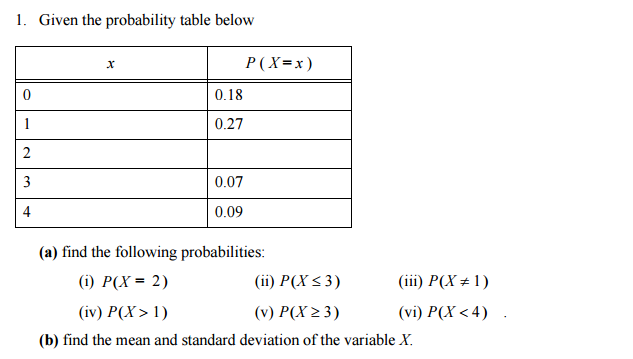
Solved Given The Probability Table Below A Find The Fol Chegg Com

Www Stat Auckland Ac Nz Fewster 210 Notes 16s2 Ch4annotated Pdf

B Find The Probability P X 2 0492 C The Probability P X 2 Is Equal To Which Of Course Hero

X Is A Binomial Variable Such As That 2p X 2 P X 3 And Mean Np Of X Is Known To Be 10 3 What Would Be The Probability That X Assumes At Most The

If A Random Variable X Follows Poisson Distribution Such That P X 1 P X 2 Then What Is P X 0 Quora

Ex 13 4 8 A Random Variable X Has Probability Distribution

2

The Random Variable X Has A Probability Distribution P X Of The Following Form Where K Is Some Number P X K If X 0 2k If X 1 3k If X

Http Www Stat Rutgers Edu Hcrane Teaching 5 Lectures Chapter12 Pgf Pdf

Parameters Of Discrete Random Variables

Www Shsu Edu Jga001 Chapter 6 1 to 6 3 alford Pdf

Suppose X Has A Poisson Distribution With A Mean Of 4 How Would I Find The Probability When X 0 X 4 X 2 And When X 8 Socratic

Probability And Random Variable Powerpoint Slides

Find Probabilities And Expected Value Of A Discrete Probability Distribution Youtube

Expected Value Of A Binomial Variable Video Khan Academy

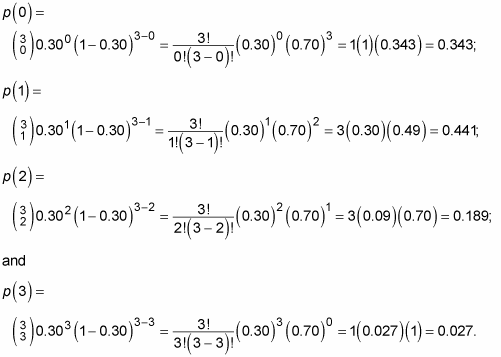
How To Find Binomial Probabilities Using A Statistical Formula Dummies

If N 5 And P 0 6 What Is The Probability That P X 2 Socratic

Parameters Of Discrete Random Variables

Answered Consider The Probability Distribution Bartleby

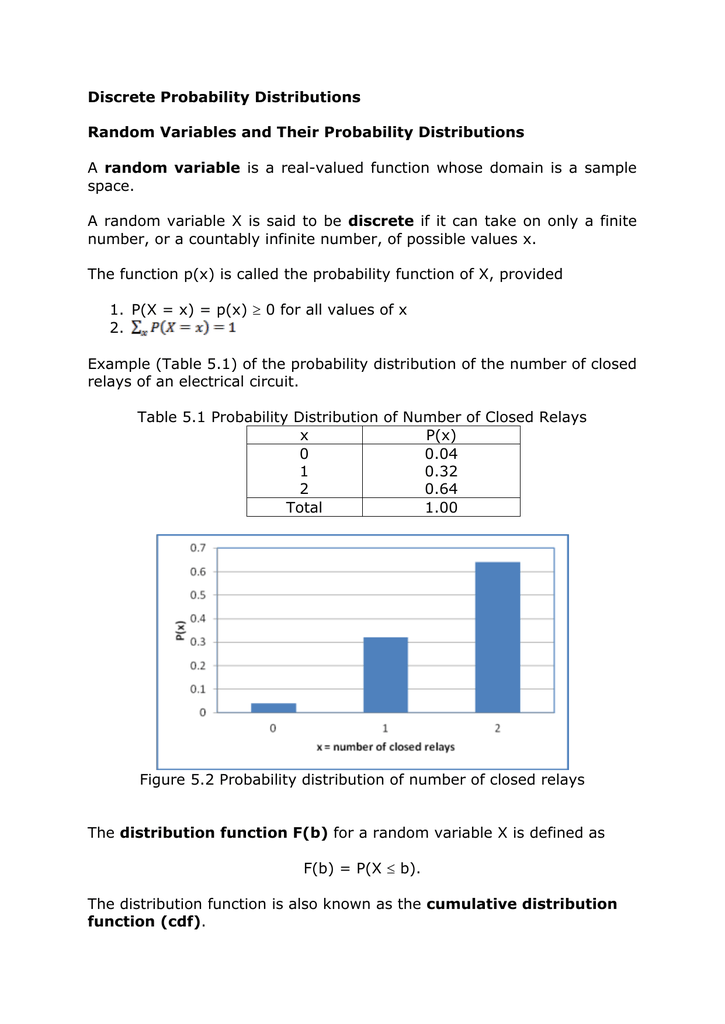
Discrete Probability Distribution

Www Srtmun Ac In Images Data Schoolcirculars Module3typesofrandomvariablesandexpectation Pdf

Probability Distribution

Www Le Ac Uk Users Dsgp1 Exercise Statsex Topics Abinome Pdf

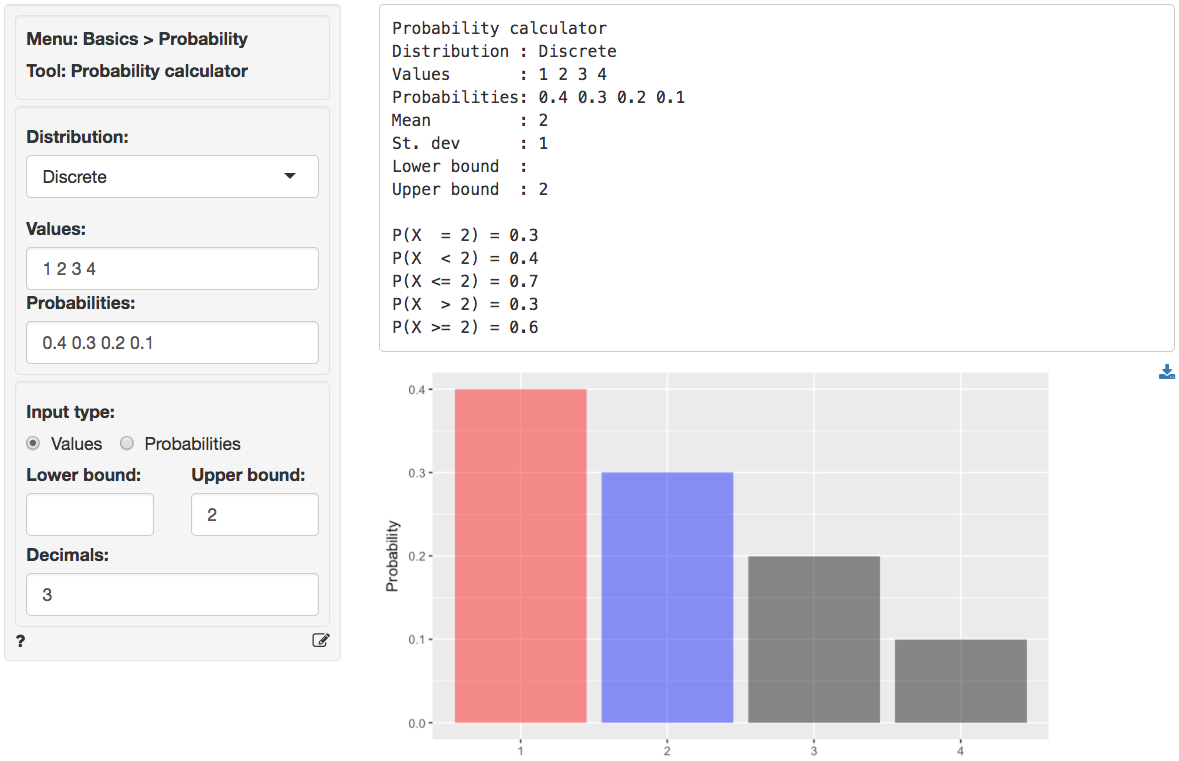
Basics Probability Probability Calculator

Solved Consider The Random Variable X With Probability Di Chegg Com

Random Variables And Probability Distributions Make Me Analyst

1

Http Abel Math Harvard Edu Ctm Home Text Class Harvard 154 11 Html Home Solns Soln8 Pdf

Use The Probability Distribution Table To Answer The Question What Is P X 2 Enter Your Answer Brainly Com

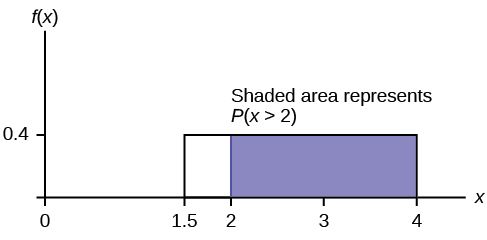
Properties Of Continuous Probability Density Functions Introductory Business Statistics

Random Variables And Probability Distribution 2 Ppt Download

The Random Variable X Has The Following Probability Distribution 1 2 3 4 P X X 0 2 0 1 0 3 K Then The Variance Of X 2 1 O 2 O 3 O 4 O 1 29 V 1 27 1 31 1 23

2

Answered Suppose X Is A Random Variable With Bartleby

The Probability Mass Function For The Discrete Random Variable X Is P X 0 0 13 P X 1 0 31 P X 2 M What Is Homeworklib

The Random Variable X Has A Probability Distribution P X O

Chapter 6 Probability Generating Functions

1 Random Variables And Probability Distributions Professor

Www Stt Msu Edu Users Makagonk 315 Week3 315notes4 1 3 Pdf

Www Stat Auckland Ac Nz Fewster 210 Notes 16s2 Ch4annotated Pdf

Conditional Probability Density Function P X 1 X 2 0 X 3 Download Scientific Diagram

Nptel Ac In Content Storage2 Courses Assignments Test Set 6 Pdf

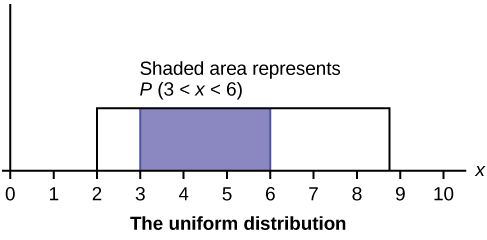
The Uniform Distribution Introduction To Statistics

Faculty Math Illinois Edu Hildebr 370 408continuous Pdf

Problems And Solutions 4

Starter The Probability Distribution Of A Discrete Random Variable X Is Given By P X R 30kr For R 3 5 7 P X R 0 Otherwise What Is The Value Ppt Video Online Download

A Factor Graph With Two Variables The Probability Function Is P X 1 Download Scientific Diagram

Www Utdallas Edu Efrom Solhw Pdf

Solved 1 The Discrete Random Variable X Has A Probabilit Chegg Com

Probability And Random Variable Powerpoint Slides

Solved Given The Following Praf Find The Following Proba Chegg Com

Solved The Random Variable X Has The Probability Distribu Chegg Com

My Ece Utah Edu Ece3530 M2soln Pdf

Q Tbn And9gctqsop5xoyrsdnd92znktpup9 Ctr1ohag3khqngrp Ali2fxrt Usqp Cau

Conf Math Illinois Edu Rsong 461f10 Lect6 Pdf

How To Calculate Probability Using The Poisson Distribution

Http Math Furman Edu Dcs Courses Math37 Lectures Lecture 13 Pdf

Solved 5 Let X Associated Probabilities P X X 2 Be Chegg Com

Probability And Random Variable Powerpoint Slides

Random Variables And Probability Distributions Ppt Video Online Download

Probability And Random Variable Powerpoint Slides

Aswarphysics Weebly Com Uploads 4 6 2 1 Advanced Level Mathematics Mechanics 1 Part4 Pdf

Bayes Theorem Some Perspectives By Garychl Towards Data Science

Q Tbn And9gcti5deikmb E9izntzmpt Gay8jhfgc 1hwh5udkl08w5s4lmri Usqp Cau

The Probability Distribution Of A Random Variable X Is Given As

Mba I Qt Unit 4 1 Introduction To Probability Distributions

What Is The Mean Of F X 3x 2 Where X Is A Random Variable With Probability Distribution X X 1 2 3 4 P X X 1 6 1 3 1 3 1 6

Free Throw Binomial Probability Distribution Video Khan Academy

2

Http Webpages Uidaho Edu Renaes 301 Lectures Module6 Pdf

Http Www Ams Sunysb Edu Linli Teaching Ams 310 Sample Final Sol Pdf

Cumulative Distribution Function Cdf

2

Probability With Discrete Random Variable Example Video Khan Academy

Incoming Term: p(x 2) probability calculator, p(x 2) probability, the probability that p(x 2) is equal to, in probability theory p(x=2) means, how to find probability p(x), how to find p probability, how to get p(x) in statistics,